Monitoring load has been a key point in team sports during last years. This study aimed to determine the relationship between the external and internal training load during full basketball practices in elite female youth basketball players.
Material and methodsThirteen elite female youth basketball players (age 16.3±1 years, height 181.7±5.8cm and body mass 71.2±9.6kg) had physical and physiological monitored over seven weeks. Players’ internal load was assessed using the session-rating of perceived exertion (sRPE), the Edward's summated heart rate zones model (SHRZ) and, the Banister's training impulse (TRIMPB). The external load was determined through: 1) total accelerations (TA); the sum of all accelerations and decelerations; 2) maximal accelerations and decelerations (TAMax); 3) total accelerations per minutes (TA·min−1); 4) accelerations per minute (Acc·min−1); and 5) decelerations per minute (Dec·min−1). Heart rate-based and accelerometry models were assessed via Polar Pro technology.
ResultsCorrelations between variables revealed different magnitudes. SHRZ model showed a positive correlation with TA (0.63); the TRIMPB model showed a high degree of correlation with TA (0.78); the sRPE model also presented a high correlation with TA (0.62).
ConclusionOur study establishes different levels of association between external and internal load models in elite female youth basketball players. However, we cannot assume that a high relationship between internal and external loads exists, as both models should be considered as different constructs.
Today, technology allows monitoring and to describe sport demands with greater precision than ever before.1–3 During the last decade, the physical demands of basketball have been described through several studies4–6; however, not many of them are explicitly related to female youth athletes. The development of smaller and more reliable devices has opened a new field of research in sports sciences, including new perspectives on the study of the physical demands and physiological responses of team sports, and specifically, within basketball contexts.4,7–9 Recent studies using technology have described basketball as a high demanding sport considering its aerobic and anaerobic requirements, its changes of direction, accelerations, decelerations, jumps, sprints, contacts and, specific skills. Thus, performance in elite basketball competition is closely related to the players’ fitness level.7 Additionally, basketball imposes significant cognitive demands surrounding decision-making and anticipatory processes.10 The measurement of the specific physical sport demands and the athlete's physiological responses, using different models, allows coaches and practitioners to obtain objective information about individual and collective training loads. The advances in the field of load monitoring are helping researchers and staff to optimize the sport-specific practices to raise player's fitness, promote specific adaptations, decrease the possibility of getting injured or experience non-functional overreaching, and overtraining syndrome or undertraining.7,8,11,12
Various models to monitor training loads in team sports exist, but the validity of these and their competitive development has important limitations. Thus far, to quantify sport demands and athletes’ responses, two different categories of load units have been utilized. External load (EL) is defined as the dose of external stimulus applied to the athlete during practices or competitions.12 In recent years, the use of global positioning systems (GPS) has become a reference method to measure EL in various field sports. However, its signal interference and imprecision in indoor sports has caused the development of local positioning systems (LPS), which are based in radiofrequency and the commercialization of devices incorporating accelerometers, gyroscopes, and magnetometers. Not many previous publications have monitored these physical demands through absolute or relative (min−1) EL variables e.g., using Player Load (PL).7,13,14 However, we can find several studies where the authors use secondary parameters derived from accelerometry, like speeds in the distances traveled15.
On the other hand, internal load (IL) is an individual response to an external stimulus, resulting in physiological and psychological stress responding to the requirements imposed on the athlete. IL can be monitored through different metrics12 such as 1) heart rate (HR), 2) oxygen uptake (VO2), 3) biochemical indicators, 4) rating of perceived exertion (RPE), and 5) questionnaires. We can also find within the literature, different indices16: 1) Banister's training impulse (TRIMPB)17; 2) session-RPE (sRPE)18; 3) Edward's summated heart rate zones model (SHRZ)19.
The models mentioned above may allow a better understanding of the specific demands of basketball and individual acute and chronic changes. Variations in acute and chronic loads are the result of the athlete's cumulative IL during the training process. The IL of each player will be affected by physical demands so that higher EL values could involve increased energy costs during and after the activity. Understanding this relationship could allow a precise periodization of team and athlete activity during the season, lengthening their sports careers, following the dose-response paradigm in sports training. For this reason, we find some studies examining this association in team sports.20,21 However, to the best of our knowledge, only one study has investigated the relationship between these models in adult basketball players8. However, no pieces of research looking for this association in female youth basketball players can be found.
To understand the relationship between internal and external loads could be a possible solution to improve the training and rehabilitation processes and managing more effectively the exposure minutes. Therefore, the main aim of this study was to determine the relationship between internal and external loads during basketball practices in elite female youth basketball players.
Material and methodsDesignThis study followed a longitudinal descriptive research design. Training loads data were collected during a seven-week in-season period (February-April) of the 2016-17 Second Division competition of the Spanish professional basketball league (LF2). Each player contributed with a mean (±SD) of 13.67±5.96 sessions. For the analysis, the inclusion criteria were: (1) to complete the basketball team-training session; and (2) to collect all the variables of the session (minutes, heart rate, sRPE, and accelerometry). Load data were collected across 35 sessions, with a total of 164 registered events.
Player internal and external load values were collected across all the basketball training sessions. Two indicators of internal load were used: HR and sRPE. Besides, the external load was calculated using players' accelerometer outputs that were measured during practices. All training sessions were indoor in similar environmental conditions.
ParticipantsThirteen elite female youth basketball players (age 16 ± 1 years, height 181 ± 6 cm and body mass 71 ± 9 kg, and 7±1 years of playing experience), participating in a basketball national player development program, volunteered for this study, and were monitored across the first seven weeks of the season (26.9% of the weeks belonging to the competitive period). All of the participants competed in the Second Division of the Spanish professional basketball league (LF2).
Before starting the study, the health of all the participants was checked by the team's physicians. Participants and their legal guardians received detailed written and verbal information about the possible risks and discomforts associated with the testing procedures. Written informed consent was obtained from all the participants and their legal guardians, respectively. Procedures performed in the study followed the Declaration of Helsinki (World Medical Association, 1964) and its later amendments.22
MethodologyInternal and external loads were assessed via Polar Pro technology (Polar Team Pro, Polar Electro Oy, Finland). These devices incorporated HR and acceleration sensors with a sampling frequency of 200 Hz. Only accelerations maintained at least 0.5 seconds were included in the analysis. Sensors were placed in the middle of the player's chest. The devices were assigned to the same athlete throughout the duration of the whole study. Following similar protocols, RPE was collected 30 minutes after each practice.
Before initiating the study, all players were familiarized with the devices and the procedures to report RPE. Additionally, before starting the data collection process, individual HRmax and basal heart rate (HRbasal) were calculated using a single test using the 30-15 Intermittent Fitness Test23 and measuring their resting heart rate for 5 minutes after waking up during 10 minutes. Before starting every basketball-specific session, players carried out a standardized warm-up with a duration of 10 min (Figs. 1 and 2).
The mean ± SD (A) individual absolute physiological responses values during practice; (B) absolute individual physical demand values during practice; and (C) relative to time external load during basketball practice (n = 164). SHRZ Score = Edward's summated heart rate zones model; TRIMPB = Banister's training impulse; sRPE = session-rating of perceived exertion; Total Accelerations = total accelerations and decelerations during practice; TAMax = sum of all maximal accelerations and decelerations; TA·min−1 = total accelerations per minute; Acc·min−1 = accelerations per minute; Dec·min−1 = decelerations per minute.
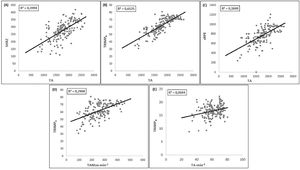
Correlations between external and internal load during practice: (A) between TA and SHRZ; (B) between TA and TRIMPB; (C) between TA and sRPE; (D) between TAMax·min−1 and TRIMPB; (E) between TAMax·min−1 and TRIMPB. (n = 164). 95% CI = 95% confidence intervals. R2 = coefficient of determination.
The internal load was determined through player HR applied to TRIMPB17 and SHRZ19 and individual rate of perceived exertion using sRPE.18 Outcomes of all models are expressed in arbitrary units (AU).
The TRIMPB model calculates the load through individual player HRmax, HRbasal, and HRmean during practice. The applied formula was the following:
Where, e = 2,712; x = (HRmean - HRbasal)] / [(HRmax - HRbasal).
SHRZ was calculated using HR based on Edwards's model.19 This model assumes as individual IL the sum of the time spent in arbitrary HR-zones weighted multiplying the accumulated time in each HR zone (in minutes) by a relative factor for each zone:
Where, zone 1 = 50-59% HRmax; zone 2 = 60-69% HRmax; Zone 3 = 70-79% HRmax; Zone 4 = 80-89% HRmax; and Zone 5 = >90% HRmax.
Each player reported their RPE individually to the researchers using the category ratio scale (CR-10) by answering the question, “How hard was the practice?” 30 min after the end of each training session.18 This value was collected using a mobile app Quanter (Kvantia, Helsinki, Finland). This method shows a good fit in HR models when compared with paper-pencil methods sRPE was obtained by multiplying the duration of each session (in minutes) by the RPE of each player.24
Where RPE = Borg's 1-10 category ratio scale.
Before starting the study, all players familiarized themselves with the RPE scale for four weeks. This model has been used consistently to monitor the psychophysiological loads in basketball.6,25
Outcomes selected to quantify EL were categorized into absolute and relative to time measurements. Absolute metrics were: 1) total accelerations and decelerations (TA) and 2) the sum of all maximal accelerations and decelerations (TAmax; >2.0 m/s2 + <-2.0 m/s2). These acceleration thresholds are similar to those used in previous male basketball research.26 The relative to time variables used were: 1) total accelerations per minute (TA·min−1); 2) accelerations per minute (Acc·min−1); 3) decelerations per minute (Dec·min−1).
Statistical analysesDue to the data sample size (n=164), the Kolmogorov-Smirnov test was used to examine if variables were normally distributed. As normality of the dataset was assumed, relationships between the internal and external load models were determined using Pearson's Rho product-moment correlation with 95% confidence intervals. Correlation magnitudes were defined according to the Hopkins's criteria27 trivial: 0-0.09; low: 0.10-0.29; moderate: 0.30-0.49; large: 0.50-0.69; very large: 0.70-0.89; nearly perfect 0.90-0.99; 1 perfect. The significance level was set at p ≤ 0.001. The coefficient of determination (R2) was determined to understand the adjustment between the control models of the external and internal load. Means (±SD) were calculated for all descriptive and outcome measures. All statistical analyses were performed using IBM Statistical Package for the Social Sciences (SPSS, version 21 for macOS, SPSS Inc, Chicago, IL).
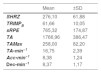
ResultsThe mean ± SD external (TA, TAmax, TA·min−1, Acc·min−1 and, Dec·min−1) and internal (TRIMPB, SHRZ, and sRPE models) loads of the basketball training events are shown in Table 1. The level of correlations and coefficients of determination between external and internal load models during basketball practices from this research study is shown in Table 1. We observed different correlation magnitudes between the internal and external models described in this research. A very large relationship was found between TA and TRIMPB model (0.78) and a large correlation between TA and SHRZ model (0.63) and sRPE model (0.62). In the case of TAmax and the observed internal methods, a moderate association with SHRZ and sRPE (0.41) and a large with TRIMPB (0.54) were observed. A moderate or lesser correlation was found between EL relative to time outcome and IL models. All relationships were statistically significant (p ≤ 0.01).
Mean ± SD values of the different methods used in practice events.
| Mean | ±SD | |
|---|---|---|
| SHRZ | 276,10 | 61,88 |
| TRIMPB | 61,66 | 10,05 |
| sRPE | 765,32 | 174,87 |
| TA | 1766,96 | 386,47 |
| TAMax | 258,00 | 82,20 |
| TA•min−1 | 16,75 | 2,39 |
| Acc•min−1 | 8,38 | 1,24 |
| Dec•min−1 | 8,37 | 1,17 |
SHRZ Score = Edward's summated heart rate zones model; TRIMP = Banister's training impulse; sRPE = session-rating of perceived exertion; TA = total accelerations and decelerations during practice; TAMax = sum of all maximal accelerations and decelerations; TA·min−1 = total accelerations per minute; Acc·min−1 = accelerations per minute; Dec·min−1 = decelerations per minute.
Correlations for external and internal workload variables. Pearson's correlation, variances, and significance.
SHRZ Score = Edward's summated heart rate zones model; TRIMP = Banister's training impulse; sRPE = session-rating of perceived exertion; TA = total accelerations and decelerations during practice; TAMax = sum of all maximal accelerations and decelerations; TA·min−1 = total accelerations per minute; Acc·min−1 = accelerations per minute; Dec·min−1 = decelerations per minute.
The main finding of this study is a low to a large correlation between models to monitor EL and IL in youth female basketball players, especially within IL models and TA. On the contrary, this research did not find significant correlations between the models related to the number of accelerations per unit of time and the IL.
This relationship, a priori, seems logical since a more significant physical demand requires the contribution of energy substrates and oxygen to the muscle tissue, increasing cardiac effort, and oxygen consumption. Despite this, there is a need to establish a proper relationship between physical demands and the physiological response of the athlete, in order to understand the dose-response relationship when training youth female basketball players.
Our findings observed a significant relationship among the studied models and various magnitudes of the relationship between external and internal load in female basketball (r = 0.21-0.78; p ≤ 0.01). Our results also display a large correlation between TA and models using heart rate activity, TRIMPB (0.78) and SHRZ models (0.63), and a large correlation between TA and sRPE (0.62). This relationship has already been shown in basketball, emphasizing that external and internal loads are two separated constructs. It seems like this correlation between load variables was not sufficient, requiring a coefficient of determination higher than 50% (r = 0.38-0.61; R2 = 0.14–0.38).8 Compared to our results, we obtained larger correlation values, but also with lower R2 values (0.045-0.613). Conversely, a meta-analysis including 13 studies on the relationship between physical demand and physiological responses in team sports, concluded showing consistent relationships between both constructs of load.20
To the authors’ knowledge, no publications are showing a correlation between TA and internal load models. However, we have found within the literature related to Player Load (PL) models, a similar parameter based on the sum of accelerations, showing in different contributions a large and very large correlation with SHRZ models [0.61 (0.38-0.77); 0.80 (0.71-0.86)].8 In the case of TRIMPB, several reports have shown a “possibly large” correlation with PL values [0.54 (0.40-0.66)].20 Regarding the perceptual model (sRPE) we observed a large correlation with TA (0.62). Considering the perceptual model (sRPE), we also observed a large correlation with the TA. In adult male basketball players, some authors have investigated this relationship between a perceptual model and PLTM (Player LoadTM) obtaining different results.8,28 Svilar28 showed a very large correlation (r=0.80; p≤0.05) while Scanlan has found a lower correlation (r=0.49; p≤0.05) between variables. Values showed by Svilar belong to Euroleague players gathered during the competitive period. We infer that these top-level players compete in most cases more than one game per week, exposing players to high-intensity competitive stress. So, it might be necessary to get a higher control of the training process, receiving smaller training doses, probably with less volume and more intensity, thus reporting greater values of external load and perceived effort, and finally obtaining higher values in correlation models. In contrast, Scanlan's study participants were semi-professional players with a lesser competitive load during weeks and maybe exposing players to different number and kind of tasks during practice, with variable volume and intensity. Despite using the same devices and gathering the same variables in both studies, the differences in correlation could be explained by the competitive level and, especially by the intensity and volume in the practices of the teams included in the sample. In the case of our results, the difference could also be explained by the sample characteristics, players with just one game per week, season period registered, type of training proposed, and the devices employed. These facts could be the reason why our results are more similar to those obtained in Scanlan's publication.
The correlations between models, previously described (EL: TA; IL: SHRZ, TRIMP, and sRPE), could be explained due to the time dependency of all the variables. Longer exposure time indicates a higher load value, with more accelerations or more heart activity that will be multiplied by time. Thus, we could suggest that all of these variables are quantifying the training or competition volume. It might be for this reason that our results are in agreement with some other authors’ results, showing a large and very large correlation between internal and external load models in basketball and other sports.8,20 On the contrary, we only found a large correlation between TAmax and TRIMPB (0.54), within internal models. This association could be explained by the fact that TRIMPB model considers the average and maximum heart rate value in every effort, so continuous and maximal accelerations could raise these parameters. The cardiovascular system works with a slight lag regarding the movements performed by the player, depending on the heart rate activity and the intensity of physical effort.29 The same occurs between TAmax and sRPE (0.41), as the main factor that modifies the perception of the athlete is the intensity and duration of the physical efforts performed, more intensity higher fatigue perceived.18
On the contrary, our results seem to have a moderate relationship between TRIMPB and SHRZ models with TA·min−1, Acc·min−1, and Dec·min−1 and show a low correlation between sRPE and these external variables (Table 1). As we have mentioned previously, SHRZ, TRIMPB, and sRPE models quantify load volume, and this might be the reason to explain the reduction of correlation value, with the results shown previously. In this case, external variables (TA·min−1, Acc·min−1, and Dec·min−1) are relative to time, and therefore, are more related to the density of load (units per minute).
The main limitation of the study is the amount of data collected. The initial data volume expected was higher, but several events were discarded during the process due to data signal inaccuracies. However, correlations were found in the study according to previous research, and new correlations and conclusions have been generated, providing these results interesting information to the scientific community and sports professionals. On the other hand, the use of heart rate and perceptual-based models could present some limitations described previously to determine team sports' physiological response.
In future investigations, it would be advisable 1) to use a bigger sample, allowing the use of other statistical tests such as R-Squared, aiming at obtaining higher predictive power between models; 2) combine other methods for the control of internal load that do not depend on heart rate or subjective methods; 3) establishing individual analyses could provide an understanding of the individual interactions within external and internal load values. Provided that the analyses are performed individually, we could find different conclusions since the physiological response to the same stimulus can differ significantly among players; 4) finally, it could be interesting to understand these relationships, specifically in competitive events.
Internal and external load models should be considered different constructs, and therefore, both must be quantified during the event (practice or competition) in youth female basketball. These results respond to the combination of many different factors within similar drills (space, number of players, number of opponents, or competition format) that contribute to determining the intensity in the context of intermittent team sports, especially in indoor team sports. For this reason, the relationship values found in the literature show significant differences.
ConclusionTo the best of our knowledge, this study is the first study aiming at establishing a relationship between external and internal loads in elite female youth basketball players. We can conclude that the assumption of strong relationships between external and internal loads in team sports can be misleading, as both models should be considered as different constructs. The findings of this study show a different level of correlation between external and internal load models, but current data highlights the importance of a continuous study of the complex relationship between physical demands and physiological responses in sports.
The current project has not received any external funding. The authors would like to give explicit thanks to the o the coaching staff and players of the Segle XXI program that kindly collaborated in the study.