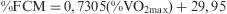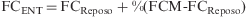El objetivo del estudio es presentar posibles aplicaciones de la frecuencia cardiaca máxima (FCM) en el entrenamiento y ambiente clínico así como identificar las ecuaciones que estiman la FCM. En el entrenamiento proporciona informaciones para la prescripción del ejercicio, el estado de sobreentrenamiento y el cálculo del gasto diario energético. En el ambiente clínico ayuda en la realización e interpretación de pruebas submaximales y maximales. En determinadas situaciones se utilizan ecuaciones matemáticas para el cálculo de la FCM. En la literatura médica especializada existen más de cincuenta ecuaciones disponibles, en las cuales solo se tiene en cuenta el factor edad o se incluyen otros factores tales como sexo, condición de salud o parámetros antropométricos. Por todo ello, para tener mayor exactitud a la hora de elegir una ecuación estimativa de la FCM es necesario conocer las existentes y optar por aquella que se adapta mejor a los objetivos de evaluación o prescripción de ejercicio.
The aim of this study was to show the possible applications of the heart rate maximum (HRmax) on training and clinical environment, as well as to identify the use of different equations to estimate the HRmax. The training provides information for the prescription of exercise, state of over-training and to calculate the daily energy expenditure. Moreover, when performed in the clinical environment they can help interpret sub-maximal tests as maximal ones. In some situations mathematical equations are used for calculating the HRmax. Thus, of more than fifty (50) equations were available in the specialised literature, some only have age as a factor, while others include, age, state of health and anthropometric parameters. However, to obtain more accuracy when choosing any equation to estimate the HRmax, one must have all the data and choose the one that best suits the objectives of evaluation or exercise prescription.
El registro de la frecuencia cardiaca (FC) es una de las formas de control fisiológico más frecuente en la evaluación de la intensidad de esfuerzo a la que el organismo está siendo expuesto1,2,3. Con el desarrollo de la técnica de control de la FC mediante el sistema Polar® se avanzó enormemente en el control de este parámetro fisiológico, ya que con esta técnica se realiza la lectura inmediata de la FC durante el ejercicio, resultando, además, más fiable que la técnica manual4.
La FC máxima (FCM) es un parámetro básico para determinar el esfuerzo y la intensidad del ejercicio. Se pueden adoptar dos maneras de registro de la FCM: la primera, considera el registro obtenido de FC más elevada tras un esfuerzo de alta intensidad5,6,7,8; la segunda, por medio de modelos estadísticos por ecuaciones que estiman la FCM de un sujeto9,10,11,12.
De manera muy extendida se suele utilizar la ecuación FCM=220–edad para estimar la FCM. Pero hay que considerar que estudios como los de Silva et al10 y Robergs y Landwehr11 apuntan que utilizar esta ecuación de manera generalizada es un error metodológico.
Se sabe que la FCM disminuye con la edad. A partir de los 20–25 años es predecible una reducción de un latido por minuto (lpm) al año13. También está bien descrito que la edad es el principal factor en modular la FCM, representando entre un 70–75%9,14. Pero cuando solamente se considera esta, es posible un aumento en la probabilidad de error del valor estimado de FCM.
Así que, además de la edad15,16, factores como obesidad17, región corporal activa durante el ejercicio (brazos o piernas)18, ambiente de registro en competición o laboratorio2,19, ejercicio en medio acuático20, nivel de entrenamiento21,22, sexo21 y acción metodológica de toma de datos23,24 son ejemplos de factores que influyen en la FCM, sugiriendo, así, el empleo de ecuaciones específicas.
Las ecuaciones estimativas iniciales de FCM fueron elaboradas a partir de diversos estudios de características transversales cuyo objetivo era determinar la curva de regresión de esta. Sin embargo, la mayor parte de las ecuaciones fueron desarrolladas para una situación de ejercicio en carrera y con hombres. Por ello, ha existido la necesidad de aumentar el abanico de actividades en que se observe la respuesta de la FCM y en mujeres.
La necesidad de establecer ecuaciones específicas para cada tipo de ejercicio también está justificada por el hecho de que actividades con un mismo consumo de oxígeno puede suponer un estímulo distinto al sistema cardiovascular. Esto está bien descrito en el trabajo de Kravitz et al25 al comparar las demandas cardiacas y metabólicas de cuatro tipos de ejercicios. Otro ejemplo sería el esfuerzo en natación, en el que se admite una disminución de 14±1,54lpm14, o incluso registros inferiores del orden de 20,25lpm en hombres y 22,1lpm en mujeres, cuando se compara con la FCM en carrera26.
La estimación del VO2max por medio de la FCM predicha por una ecuación inadecuada puede producir importantes errores a la hora de prescribir un entrenamiento: cargas de entrenamiento sin efectividad para proporcionar adaptaciones orgánicas o cargas extremadamente elevadas que pueden contribuir a desarrollar un estado de sobreentrenamiento27. La realización de ejercicio por encima de la intensidad ideal puede producir una disminución inmunológica, con reducción de la resistencia viral, además de predisponer al deportista a un estado de síndrome de fatiga crónica22.
Por todo lo expuesto, el objetivo del presente documento ha sido realizar una revisión sobre las aplicaciones de la respuesta de la FCM en el entrenamiento y en el ambiente clínico, así como identificar las ecuaciones que estiman la FCM.
Aplicaciones de la frecuencia cardiaca máximaLa FCM es una variable cardiovascular que ofrece una serie de informaciones tanto a la hora de evaluar una prueba física como de prescribir un entrenamiento. Veamos estas aplicaciones con más detalle con el fin de mejorar la acción profesional.
Existen varias formas de control de la intensidad del ejercicio: formas simples, como la escala de percepción subjetiva del esfuerzo de Borg, o más complejas, como la toma de muestras sanguíneas seriadas para conocer los niveles de ácido láctico y detectar el umbral anaeróbico. No obstante, la toma de FC supone una excelente forma de control y seguimiento del ejercicio, siendo empleada para las poblaciones más diversas: sedentarios, deportistas, personas mayores y enfermos cardiacos, además de atletas infantiles de élite1,6,19,22,28,29,30. El empleo de la FC como procedimiento de control de la carga de entrenamiento se justifica por ser de sencillo registro (manual o sistema de registro telemétrico con pulsómetros) y, principalmente, por el hecho de que existe una correlación entre los valores de la FCM y el VO231. Estos factores hacen posible que se pueda establecer un programa de actividad física que tome la FC como elemento de control de la intensidad del ejercicio32. Con este control se puede establecer la actividad física de forma individualizada.
Kesaniemi et al29 han establecido unas pautas para determinar la intensidad del ejercicio, tomando como base la FC de reserva, el VO2max de reserva y la FCM absoluta, además del índice de percepción subjetiva de esfuerzo, más conocido como índice de Borg. El primer factor que debe ser observado a la hora de calcular la intensidad es el nivel de actividad que presentan los sujetos, diferenciando entre deportistas y personas con un nivel de actividad física normal (tabla 1).
Tabla 1. Propuesta para cálculo de intensidad de entrenamiento
| Deportista | Adultos saludables | |||
| Intensidad | %VO2Ra | %VO2Ra | %FCMc | RPE |
| %FCR b | %FCR b | |||
| Muy fácil | <50 | <20 | <50 | <10 |
| Fácil | 50–65 | 20–39 | 50–63 | 10–11 |
| Moderado | 65–75 | 40–59 | 64–76 | 12–13 |
| Difícil | 75–90 | 60–84 | 77–93 | 14–16 |
| Muy difícil | 90–95 | ≥85 | ≥94 | 17–19 |
| Máximo | 95–100 | 100 | 100 | 20 |
FCM: frecuencia cardiaca máxima; RPE: índice de percepción de esfuerzo.
a %VO2R: porcentaje de trabajo teniendo en cuenta al VO2 de reserva.
b %FCR: porcentaje de trabajo teniendo en cuenta al VO2 de reserva.
c %FCM: porcentaje de trabajo tomando como referencia la FCM registrada o calculada (Kesaniemi et al, 2001) 29 .
En la tabla anterior se muestra cómo es posible emplear la FC como parámetro de cálculo de intensidad del entrenamiento, observando la correlación existente entre la FC de reserva y el VO2max de reserva. Por otra parte, los mismos autores afirman que si se tomase en consideración solamente la FCM, variaría la estimación de la curva de regresión, siendo necesario emplear la ecuación:
En la propuesta de Karvonen et al33 se define el concepto de FC de reserva como la resultante de restar a la FCM la FC de reposo. Por medio de esta fórmula se puede establecer la FC de entrenamiento (FCENT) pretendida mediante la aplicación de la siguiente ecuación:
La ecuación anterior permite establecer rangos de esfuerzo teniendo en cuenta umbrales metabólicos, en especial el umbral anaeróbico de 4mmol/l−1, que está a su vez relacionado con la FCENT. Se dispone, así, de valores mínimos o máximos de FC que deben ser seguidos por el deportista a lo largo de su entrenamiento. Esto permitirá que tenga mayor éxito deportivo, ya que entrenará de manera más adecuada.
Una de las variables para estimar la FCENT es la FCM. Pero no siempre es viable llevar a cabo una prueba máxima para obtenerla (personas muy desentrenadas, enfermedades que contraindican esfuerzos máximos, etc.). En estas situaciones se utilizan ecuaciones matemáticas para el cálculo de la FCM.
Hay que destacar que la FCM estimada, además de ser utilizada como parámetro de control de la intensidad del ejercicio, es un factor que sirve como indicador de otros parámetros en el ejercicio. La primera aplicación es utilizarla como referente para estimar el VO2max durante una prueba submaximal, como las pruebas de tapiz de Waddoups et al34, Faulkner et al35 o Ebbeling et al36, además de la tradicional prueba en cicloergómetro de Astrand y Ryhming37. En este sentido, Uth et al38 propusieron una ecuación para estimar el VO2max tomando como base la FCM y la FC de reposo en sujetos deportistas de entre 21–51 años. Una segunda utilidad aplicada a los estudios de gasto diario energético sería calcular la energía consumida tomando como base un porcentaje del trabajo de la FCM39,40.
Como tercera aplicación, la FCM serviría para la interrupción del esfuerzo en una prueba ergométrica1,3,8,41,42. Además, el Colegio Americano de Cardiología, junto con la Asociación Americana del Corazón (200243), consideran que no superar el 80–85% de la FCM prevista durante una prueba ergométrica es un indicio claro de la existencia de coronopatía. También se considera importante, tras obtener la FCM, observar la respuesta de la recuperación. Es necesaria una disminución de la FC del orden de 12lpm tras 2min de recuperación; en el caso de que no se produzca este descenso, también es previsible la existencia de algún problema cardiaco.
Otra aplicación de la FCM es determinar si una prueba ergométrica ha sido realizada con un esfuerzo máximo, si se observa que el evaluado presenta, en el último registro de la FC, una variación de 10lpm con la FCM calculada41,42. La FCM también puede servir para estimar umbrales metabólicos durante una prueba maximal44. Por último, se debe tener en cuenta que una disminución en la FCM de 5lpm puede indicar un estado de sobreentrenamiento45.
La FCM proporciona, así, un conjunto de factores de análisis tanto para la prescripción del ejercicio como para condiciones de ambiente clínico de evaluación física. Es muy importante un conocimiento profundo sobre este parámetro fisiológico para su correcta interpretación.
Ecuaciones predictivas para estimar la frecuencia cardiaca máximaSe considera a Robson (1938), citado por Londeree y Moeschberger14, como el primero en establecer una ecuación que relaciona la edad con la FCM (FCM=212–0,775 edad). Sin embargo, la fórmula más extendida en el campo de la medicina del deporte y del entrenamiento deportivo es la que considera la FCM=220–edad46,47,48.
Se han realizado diversos estudios de características transversales con el fin de determinar la recta de regresión de la FCM. Marins y Delgado7 presentan un resumen de estos trabajos, donde tan solo se considera como factor de la ecuación la edad (tabla 2).
Tabla 2. Resumen de ecuaciones para cálculo de la frecuencia cardiaca máxima
| Ecuación | Estudio | n | Población | Fórmula de regresión |
| 1 | ACSM (1995) | FCM=210–0,5 edad | ||
| 2 | Astrand – cicloergómetro | 100 | Hombres asintomáticos | FCM=211–0,922 edad |
| 3 | Astrand | FCM=216–0,84 edad | ||
| 4 | Bal State University | Hombres | FCM=214–0,8 edad | |
| 5 | Bal State University | Mujeres | FCM=209–0,7 edad | |
| 6 | Brick (1995) | Mujeres | FCM=226-edad | |
| 7 | Bruce et al (1974) | 1.295 | Enfermedad coronaria | FCM=204–1,07 edad |
| 8 | Bruce et al (1974) | 2.091 | Hombres asintomáticos | FCM=210–0,662 edad |
| 9 | Bruce et al (1974) | 1.295 | Enfermedad coronaria | FCM=204–1,07 edad |
| 10 | Bruce et al (1974) | 2.091 | Hipertensión+enfermos coronarios | FCM=210–0,662 edad |
| 11 | Cooper | 2.535 | Hombres asintomáticos | FCM=217–0,845 edad |
| 12 | Ellestad | 2.583 | Hombres asintomáticos | FCM=197–0,556 edad |
| 13 | Engels et al (1998) | 104 H y 101 M | Hombres y mujeres | FCM=213,6–0,65 edad |
| 14 | Fernandez (1998) | Hombres | FCM=200–0,5 edad | |
| 15 | Fernandez (1998) | Mujeres | FCM=210–edad | |
| 16 | Fernhal et al (2001) | 276 | Retardo mental | FCM=189–0,56 edad |
| 17 | Fernhal et al (2001) | 296 | Hombres y mujeres asintomáticos | FCM=205–0,64 edad |
| 18 | Froelicher y Myers(2000) | 1.317 | Hombres asintomáticos | FCM=207–0,64 edad |
| 19 | Graettinger et al (1995) | 41 | Hipertensos | FCM=200–0,71 edad |
| 20 | Graettinger et al (1995) | 114 | Hombres asintomáticos | FCM=199–0,63 edad |
| 21 | Graettinger et al (1995) | 73 | Normotensos | FCM=197–0,63 edad |
| 22 | Hammond | 156 | Enfermedad coronaria | FCM=209-edad |
| 23 | Hakki (1983) | Hombres | FCM=205–0,5 edad | |
| 24 | Hossack y Bruce (1982) | 104 | Mujeres asintomáticas | FCM=206–0,597 edad |
| 25 | Hossack y Bruce (1982) | 98 | Hombres asintomáticos | FCM=227–1,067 edad |
| 26 | Inbar et al (1994) | 1.424 | Hombres | FCM=205,8–0,685 edad |
| 27 | Jones et al (1985) – cicloergómetro | 100 | Hombres y mujeres asintomáticos | FCM=202–0,72 edad |
| 28 | Jones et al (1975) | Hombres y mujeres asintomáticos | FCM=210–0,65 edad | |
| 29 | Jones et al (1985) | 60 | Mujeres asintomáticas | FCM=201–0,63 edad |
| 30 | Karvonen et al | Hombres y mujeres asintomáticos | FCM=220–edad | |
| 31 | Lester et al (1968) | 42 | Hombres y mujeres entrenados | FCM=205–0,41 edad |
| 32 | Lester et al (1968) | 148 | Hombres y mujeres sedentarios | FCM=198–0,41 edad |
| 33 | Londeree y Moeschberger (1982) | Deportista de nivel nacional | FCM=206,3–0,711 edad | |
| 34 | Miller et al (1993) | 51 | Hombres y mujeres de peso normal | FCM=217–0,85 edad |
| 35 | Miller et al (1993) | 35 | Hombres peso normal | FCM =219–0,85 edad |
| 36 | Miller et al (1993) | 16 | Mujeres de peso normal | FCM=218–0,98 edad |
| 37 | Morris | 1.388 | Enfermedad coronaria | FCM=196–0,9 edad |
| 38 | Morris | 244 | Hombres asintomáticos | FCM=200–0,72 edad |
| 39 | Ricard et al (1990) | 193 | Hombres y mujeres | FCM=209–0,587 edad |
| 40 | Ricard et al (1990) – cicloergómetro | 193 | Hombres y mujeres | FCM=205–0,687 edad |
| 41 | Robinson | 92 | Hombres asintomáticos | FCM=212–0,775 edad |
| 42 | Rodeheffer et al (1984) | 61 | Hombres asintomáticos | FCM=214–1,02 edad |
| 43 | Rodeheffer et al (1984) – cicloergómetro | 47 H y 14 M | Hombres y mujeres | FCM=208,19–0,95 edad |
| 44 | Schiller et al (2001) | 53 | Mujeres hispánicas | FCM=213,7–0,75 edad |
| 45 | Schiller et al (2001) | 93 | Mujeres caucásicas | FCM=207–0,62 edad |
| 46 | Sheffield et al (1978) | 95 | Mujeres | FCM=216–0,88 edad |
| 47 | Tanaka et al (1997) | 84 | Mujeres entrenadas resistencia aeróbica | FCM=199–0,56 edad |
| 48 | Tanaka et al (1997) | 72 | Mujeres sedentarias | FCM=207–0,60 edad |
| 49 | Tanaka et al (2001) | 285 | Hombres y mujeres sedentarias | FCM=211–0,8 edad |
| 50 | Tanaka et al (2001) | Hombres y mujeres activas | FCM=207–0,7 edad | |
| 51 | Tanaka et al (2001) | 229 | Hombres y mujeres entrenados de resistencia | FCM=206–0,7 edad |
| 52 | Tanaka et al (2001) | 18.712 | Hombres y mujeres | FCM=208,75–0,73 edad |
| 53 | Whaley et al (1992) | 1.256 | Hombres | FCM=213–0,789 edad |
| 54 | Whaley et al (1992) | 754 | Mujeres | FCM=208,8–0,723 edad |
| 55 | Whyte et al (2008) 21 | 92 | Hombres jóvenes deportistas de competición | FCM=202–0,55 edad |
| 56 | Whyte et al (2008) 21 | 76 | Mujeres jóvenes deportistas de competición | FCM=216–1,09 edad |
Edad expresa en años (Marins y Delgado 7 ).
FCM: frecuencia cardiaca máxima; H: hombres; M: mujeres.
En la tabla 2 la edad es considerada como principal factor para la construcción de la recta de tendencia de disminución de la FCM. Pero algunos autores añaden más información al establecer, además de la edad, un perfil poblacional específico. Se han propuesto ecuaciones para personas con algún tipo de enfermedad de tipo coronario como las indicadas en las ecuaciones número 7, 9, 10, 22 y 37, o para personas con hipertensión, como son los casos de las ecuaciones 10 y 19, así como para personas con problemas neurológicos, como retardo mental49.
Otros autores se concentraron en proponer ecuaciones para personas asintomáticas, pero diferenciando el factor sexo. Este es el caso de las ecuaciones 2, 4, 8, 11, 12, 14, 18, 20, 23, 25, 26, 35, 38, 41, 42 y 53, desarrolladas para los hombres, mientras que las ecuaciones 5, 6, 15, 24, 29, 36, 44, 45, 46, 48 y 54 fueron propuestas solamente para mujeres (tabla 2). Para algunos autores, el factor sexo no influye en la respuesta de la FCM y por dicha razón presentan una ecuación única; son ejemplos las ecuaciones número 13, 17, 27, 28, 30, 31 32, 33, 34, 39, 40, 43, 49, 50, 51 y 52. Atendiendo a esta situación, sería necesario profundizar en investigación sobre el grado de influencia del factor sexo en la FCM.
También existen ecuaciones que consideran el factor etnia, como por ejemplo la ecuación número 44 para mujeres hispánicas y la 45 para mujeres caucásicas. En ningún caso se ha especificado para persona asiática o incluso indígena. El abanico de investigaciones en este sentido es muy restringido, lo que hace necesario estudios que permitan contrastar la influencia en la FCM de los factores étnicos.
En cuatro trabajos se ha investigado la etnia como un posible factor determinante en la FCM. En el primer estudio, desarrollado por Londeree y Moeschberger14, se propone un coeficiente en la ecuación. Wilmore et al50 comparó a blancos y negros americanos, observando diferencias entre los dos grupos.
El trabajo elaborado por Schiller et al51 especifica una ecuación para mujeres hispanas y otra para caucásicas. En el grupo de hispanas se observó un descenso de 0,75lpm al año, mientras que para el segundo grupo la reducción fue menor, del orden de 0,62lpm al año. Aunque estos resultados estadísticos no presentaron diferencias significativas, los autores formularon ecuaciones específicas para cada grupo. Por último, Weston et al52 no identificó diferencias en la FCM de corredores negros africanos y hombres caucásicos.
Hay ecuaciones específicas para el nivel de capacidad física, como por ejemplo las ecuaciones número 31, 33, 47, 50, 51, 52 y 55 destinadas a personas entrenadas. Por otro lado, las ecuaciones número 32, 48 y 49 son ecuaciones específicas para personas sedentarias. El nivel de aptitud física (sedentario vs. deportista) parece predeterminar una respuesta diferente en la FCM. Zavorsky22 realizó un estudio de revisión sobre este tema, en el que observó que un deportista posee, como media, 8lpm menos de FCM que una persona sedentaria, lo que podría justificar una ecuación específica para este colectivo. Estas diferencias pueden ser causadas porque las personas entrenadas comparadas con personas sedentarias poseen un mayor volumen sistólico, lo que ocasiona una reducción del número máximo de latidos cardiacos. Por tanto, para personas altamente entrenadas es muy necesario considerar el empleo de ecuaciones específicas.
El índice de masa corporal (IMC) fue considerado un factor determinante en la respuesta de la FCM cuando se considera un estado de obesidad. Para personas con IMC normal se proponen las ecuaciones 34, 35 y 36 (tabla 2), mientras que para personas con IMC igual o superior a 30kg/m2 se proponen las ecuaciones específicas descritas en la tabla 3. Esto es muy importante principalmente a la hora de establecer la intensidad de entrenamiento o durante una prueba física como criterio de interrupción.
Tabla 3. Ecuaciones para estimar la frecuencia cardiaca máxima empleando multivariables
| n | Ecuaciones |
| 1 | FCM=162+0,266 FCReposo+0,164 FC del 3min ejercicio−0,7 edad |
| Sheffield et al 59 | |
| 2 | 196,7+1,986C2+5,361E+1,490F4+3,730F3+4,036F2−0,0006A4−0,542 A2 |
| Londeree y Moeschberger 14 | |
| 3 | FCM=108,481+0,5108 RPE15−0,6570 8 FC * +0,6075 10 FC * −0,2641 edad |
| Johnson y Prins 60 | |
| 4 | Hombres: FCM=203,9−0,812 edad+0,276 FCReposo−0,084 PC−4,5 CF |
| Whaley et al 61 | |
| 5 | Mujeres: FCM=204,8−0,718 edad+0,162 FCReposo−0,105 PC−6,2 CF |
| Whaley et al 61 | |
| 6 | Hombres obesos: FCM=198–0,44 edad |
| Miller et al 62 | |
| 7 | Mujeres obesas: FCM=200–0,49 edad |
| Miller et al 62 | |
| 8 | Hombres y mujeres obesos: FCM=200–0,48 edad |
| Miller et al 62 | |
| 9 | FCM=236–0,72 edad−6,8 dimensión del ventrículo izquierdo |
| Graettinger et al 63 |
A2: edad2; A4: edad4/1.000; C2: continente (1 para Europa y 0 para otros); CF: código de fumadores (1 para fumador y 0 para no fumador); E: ergómetro (1 para tapiz y 0 para cicloergómetro); F2: nivel físico (1 para sedentario y 0 para otros); F3: nivel de actividad (1 para activo y 0 para otros); F4: nivel de resistencia aeróbica (1 para alto nivel y 0 para otros); FC: frecuencia cardiaca; FCM: frecuencia cardiaca máxima; PC: peso corporal.
* FC durante el 8.o y 10.o min del protocolo de Balke en tapiz.
A pesar de que se ha observado claramente que la FCM obtenida en carrera sobre tapiz rodante presenta valores significativamente mayores a los obtenidos en cicloergómetro, solamente se han formulado cuatro ecuaciones específicas para ciclismo (tabla 2), por lo que dicha temática debe seguir siendo objeto de investigación. No se identificaron propuestas de ecuaciones para otras formas de ejercicio, como remo o natación, que por su respuesta de inmersión necesitan muy probablemente una ecuación específica.
Los estudios26,53,54,55 que compararon la FCM en un ejercicio de natación con la obtenida en un ejercicio de carrera indican una considerable diferencia entre los resultados, con una FCM menor de entre 10–22 latidos en el ejercicio de natación. Más recientemente, Mazzeo y Tanaka56 han señalado que en los ejercicios realizados en el agua se produce una braquicardia en la FCM del orden de 10lpm, siendo necesario restar estos valores en las ecuaciones formuladas para un medio terrestre. Así que la gran mayoría de las ecuaciones propuestas solamente han abarcado el ejercicio de carrera. Esto permite un gran abanico de posibilidades de estudios exploratorios sobre la FCM en diferentes formas de ejercicio físico. Veamos algunos ejemplos.
La ecuación FCM=208,75–0,73 edad12 se considera la más adecuada para la población general de entre 18–30 años para ejercicio en carrera, tanto para hombres como para mujeres7. El trabajo de Marins et al (2007)57 apuntó que para esfuerzos en bicicleta en personas sin perfil competitivo las ecuaciones más adecuadas fueron para hombres FCM=202–0,72 edad58 y para mujeres FCM=189–0,56 edad49. Más recientemente, Whyte et al21 han propuesto dos ecuaciones para deportistas jóvenes según el factor sexo, como se puede apreciar en la tabla 2.
Algunos autores propusieron ecuaciones con modelos de regresión múltiple que son más complejos, añadiendo otra variable además de la edad (tabla 3). Son ejemplos las ecuaciones de Sheffield et al59, que añaden en la ecuación un factor que corresponde a la FC submaximal en tapiz; Londeree y Moeschberger14, que consideran la etnia, el tipo de ergómetro, el nivel físico y el tipo de protocolo; Johnson y Prins60, que consideran la percepción subjetiva de esfuerzo y FC submaximal; Whaley et al61, que proponen la FC en reposo, el peso corporal y el tabaquismo; Miller et al62, para personas con IMC superior al 30kg/m2, y Graettinger et al63, que proponen la dimensión del ventrículo izquierdo o delta epinefrina. Más recientemente, Karavirta et al64 establecen también una influencia de la variabilidad de la FC. Estos trabajos son ejemplos en los que se han tomado en consideración otras variables, además de la edad, para el cálculo de la FCM, mejorando así la exactitud de sus ecuaciones frente a la típica de 220–edad, que puede llegar a presentar un margen de error de 45lpm14.
A la hora de utilizar una ecuación para estimar la FCM con los objetivos de prescripción de ejercicio, control del entrenamiento o análisis clínico es fundamental conocer las características del deportista o evaluado con el fin de proceder a la elección adecuada de la ecuación estimativa de la FCM, mejorando así la acción profesional. Adoptar una ecuación única para todos los casos y los ambientes solamente por tradición o costumbre no parece ser una actitud correcta.
ConclusionesLa FCM proporciona una importante gama de informaciones aplicadas tanto al entrenamiento deportivo como al ambiente clínico de evaluación física. En el caso de utilizar una ecuación para estimar la FCM se debería realizar tras un análisis crítico, ya que existe un gran número de ecuaciones que han sido propuestas para diferentes grupos de población, como por ejemplo personas con enfermedad coronaria, hipertensos, con retraso mental, obesos, así como para hombres y mujeres, además de para deportistas o sedentarios. Por tanto, es necesario seleccionar aquella ecuación que estime con mayor exactitud la FCM, para que en el ámbito del entrenamiento deportivo no se cometan errores metodológicos graves en la planificación, y para que en el ámbito clínico se valore el estado de la persona y se prescriba el ejercicio físico con máxima seguridad.
Conflicto de interesesLos autores declaran no tener ningún conflicto de intereses.
Recibido 16 Marzo 2010
Aceptado 30 Abril 2010
Autor para correspondencia. jcbouzas@ufv.br